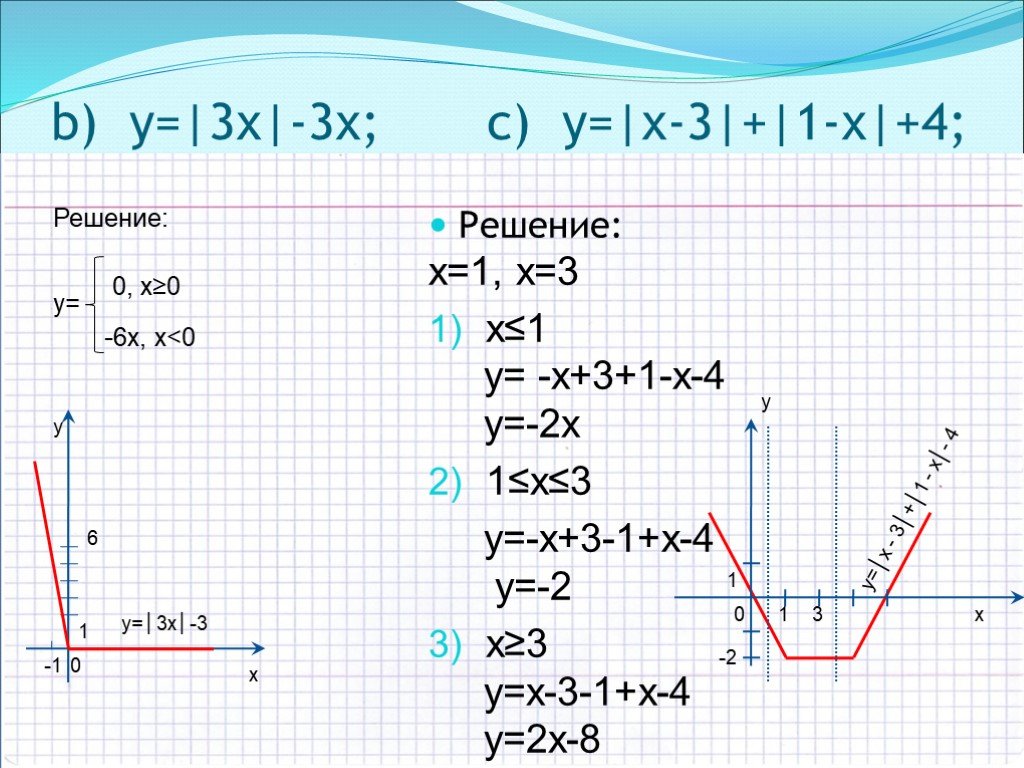
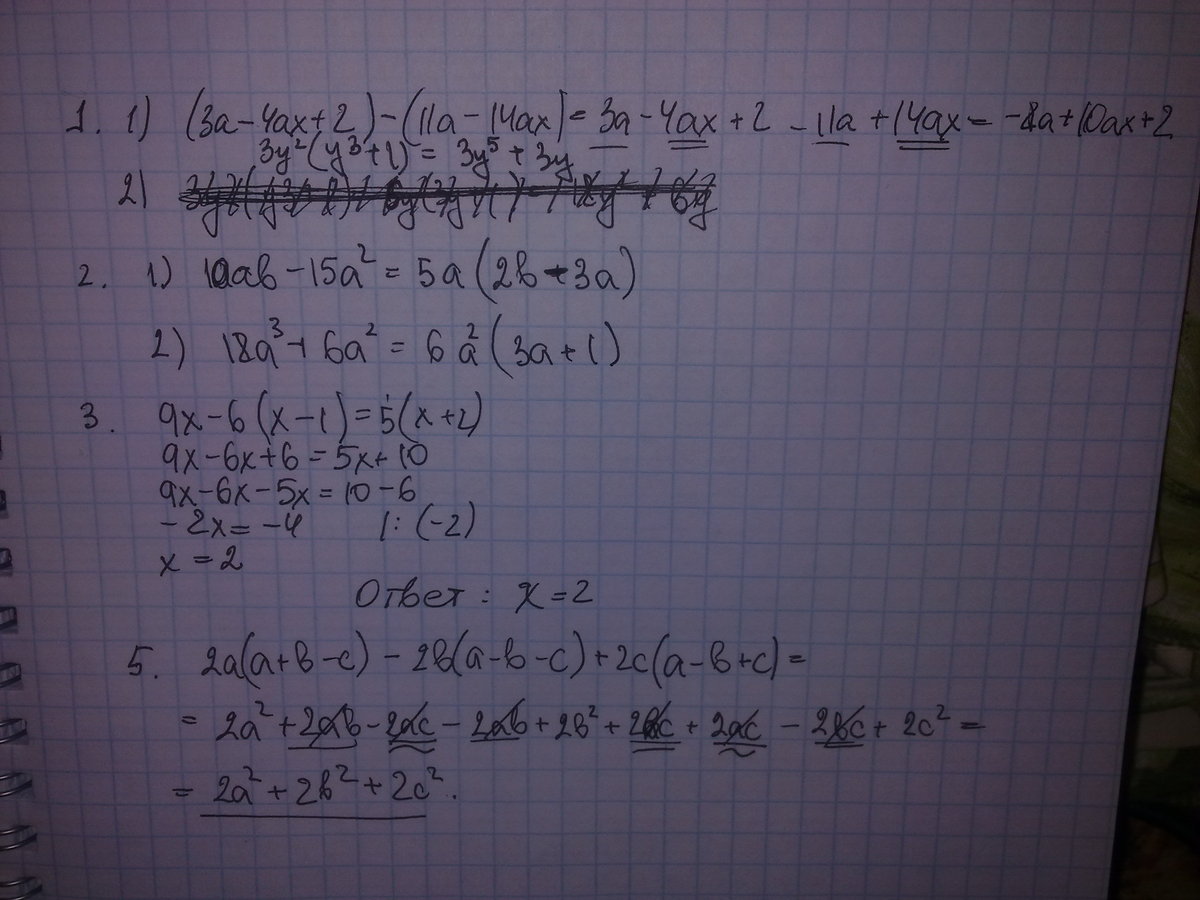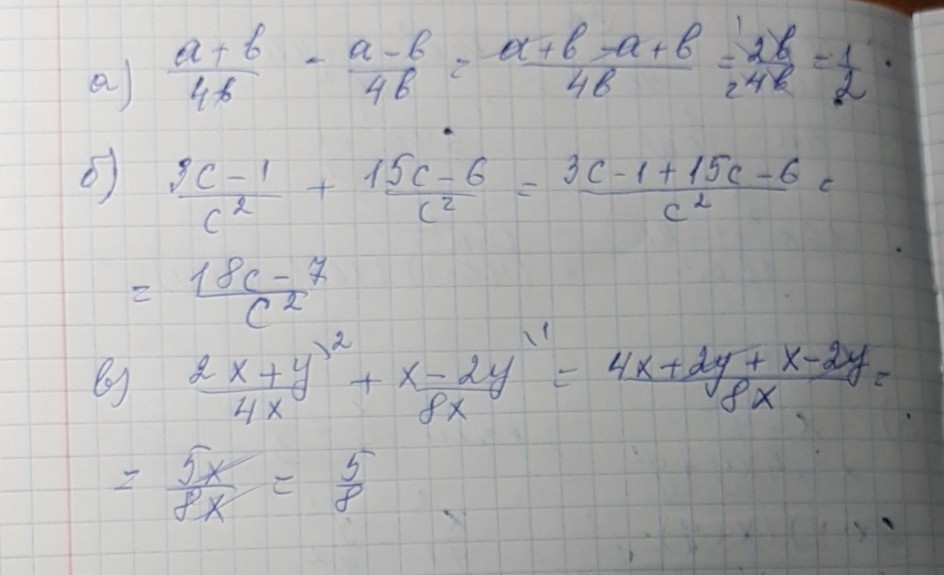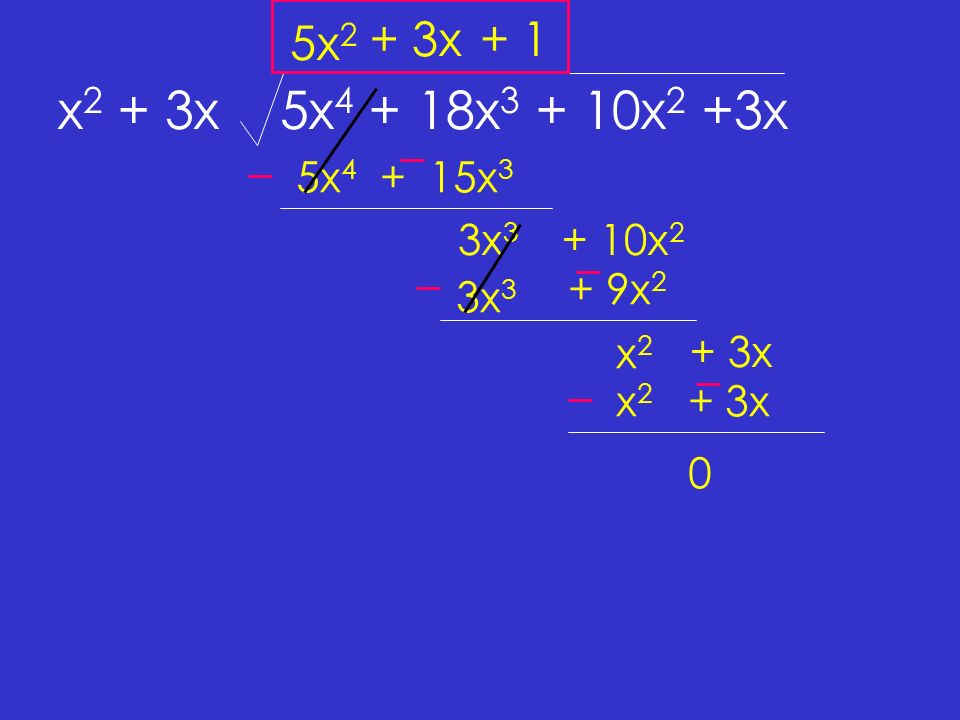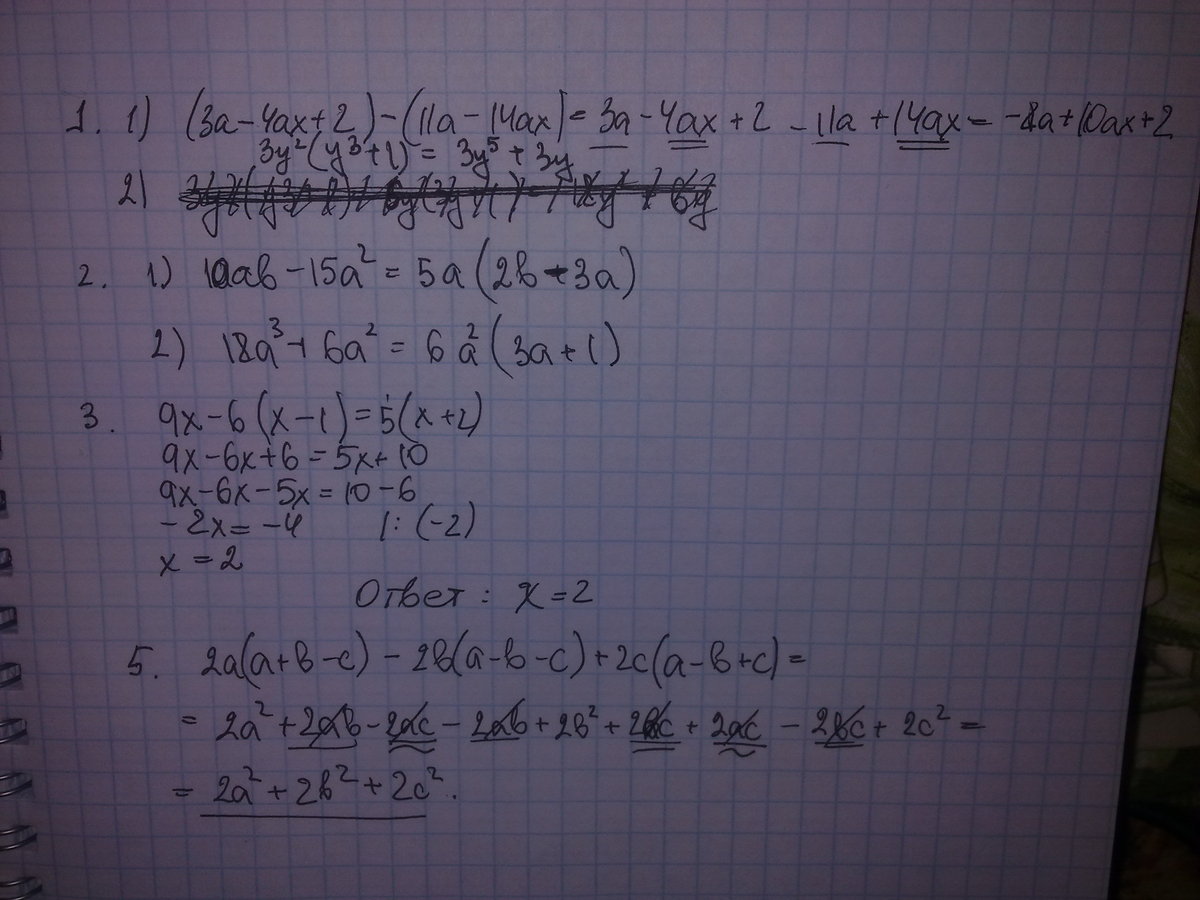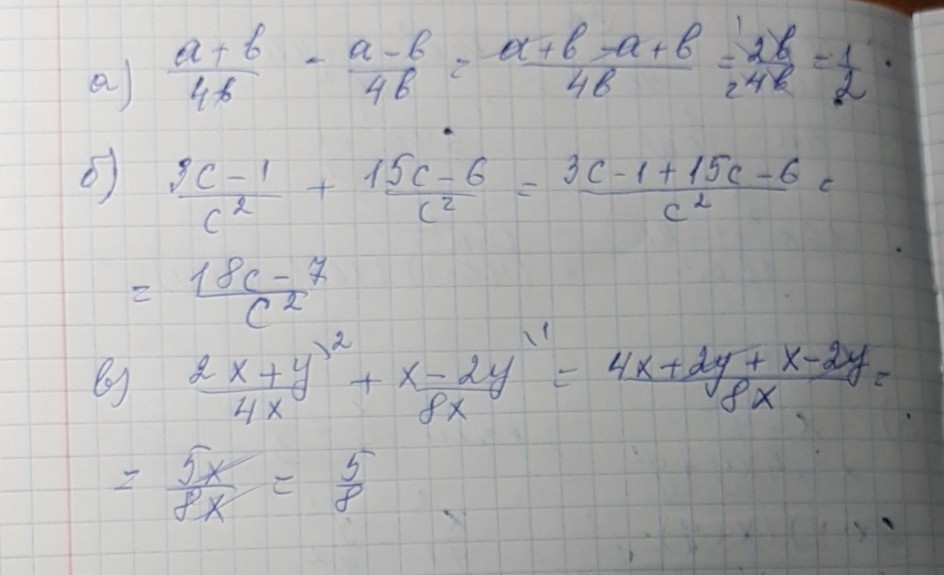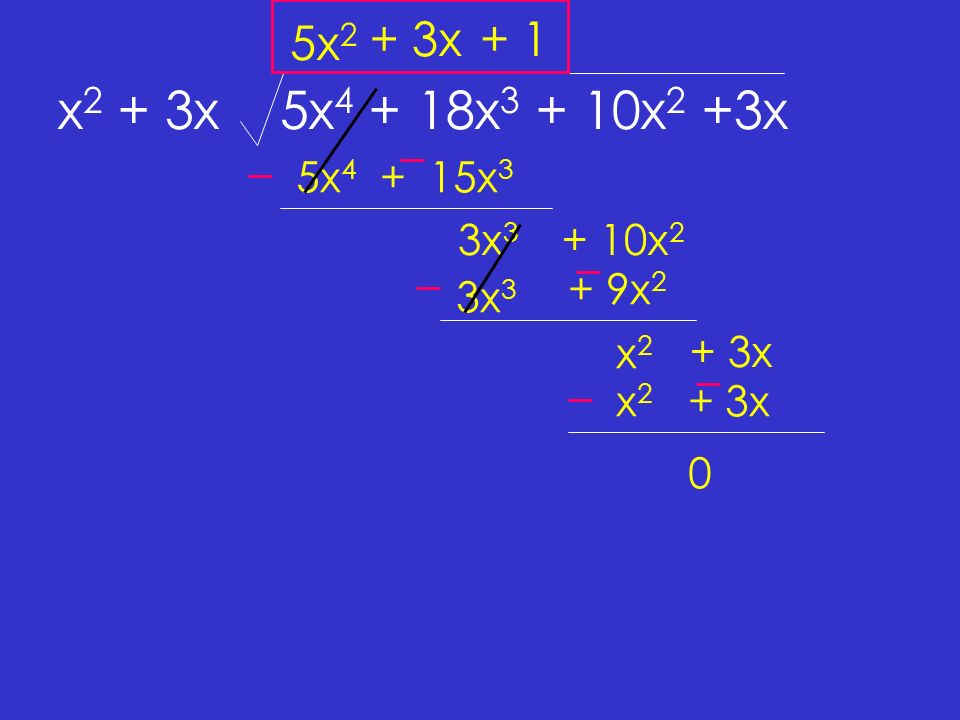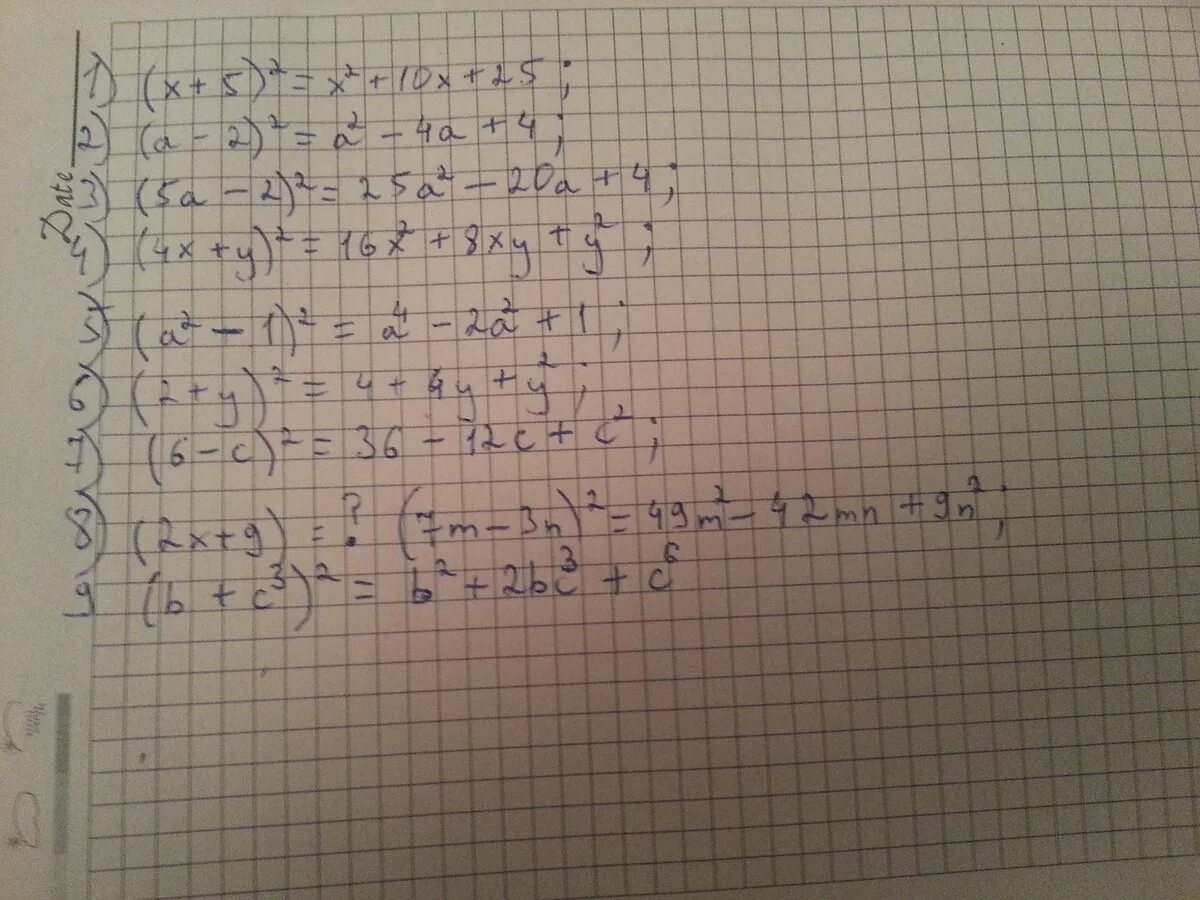 Y=|x+3|+|1-x|. 3a 3x 1 3x 1. (x6 1,2ab 5ab. Выполните преобразование по соответствующей формуле. Б) x2+3x-4=0 x1=1.
Y=|x+3|+|1-x|. 3a 3x 1 3x 1. (x6 1,2ab 5ab. Выполните преобразование по соответствующей формуле. Б) x2+3x-4=0 x1=1.
|
 8x 3 3x 8 + 9 решение. X4+x2+1 : x2-4x+5. 3a 3x 1 3x 1. 3a 3x 1 3x 1. 3x+1.
8x 3 3x 8 + 9 решение. X4+x2+1 : x2-4x+5. 3a 3x 1 3x 1. 3a 3x 1 3x 1. 3x+1.
|
 При k = -2,5t = 7,2 выражение |k|. 2х-5y=2 3x-11y=5. Если k1=k2. 3a 3x 1 3x 1. Упростить выражение k-4/k-2:(80k/k³-8+2k/k²+2k+4-k-16/2-k)-6k+4/(4-x)².
При k = -2,5t = 7,2 выражение |k|. 2х-5y=2 3x-11y=5. Если k1=k2. 3a 3x 1 3x 1. Упростить выражение k-4/k-2:(80k/k³-8+2k/k²+2k+4-k-16/2-k)-6k+4/(4-x)².
|
 14а4в/49а3в2. 3a 3x 1 3x 1. 3a 3x 1 3x 1. 2x+3xy вынести за скобки. Y=1/3x.
14а4в/49а3в2. 3a 3x 1 3x 1. 3a 3x 1 3x 1. 2x+3xy вынести за скобки. Y=1/3x.
|
 (x2+3x+1)(x2+3x+1)=-1. Vx -2x+1 ≥ 2х - 3. 3x√(x^2-x-2)<=x^2-x-2. ((3x^2-x+1)/(2x^2+x+1))^((x^3)/(1-x)). 3a 3x 1 3x 1.
(x2+3x+1)(x2+3x+1)=-1. Vx -2x+1 ≥ 2х - 3. 3x√(x^2-x-2)<=x^2-x-2. ((3x^2-x+1)/(2x^2+x+1))^((x^3)/(1-x)). 3a 3x 1 3x 1.
|
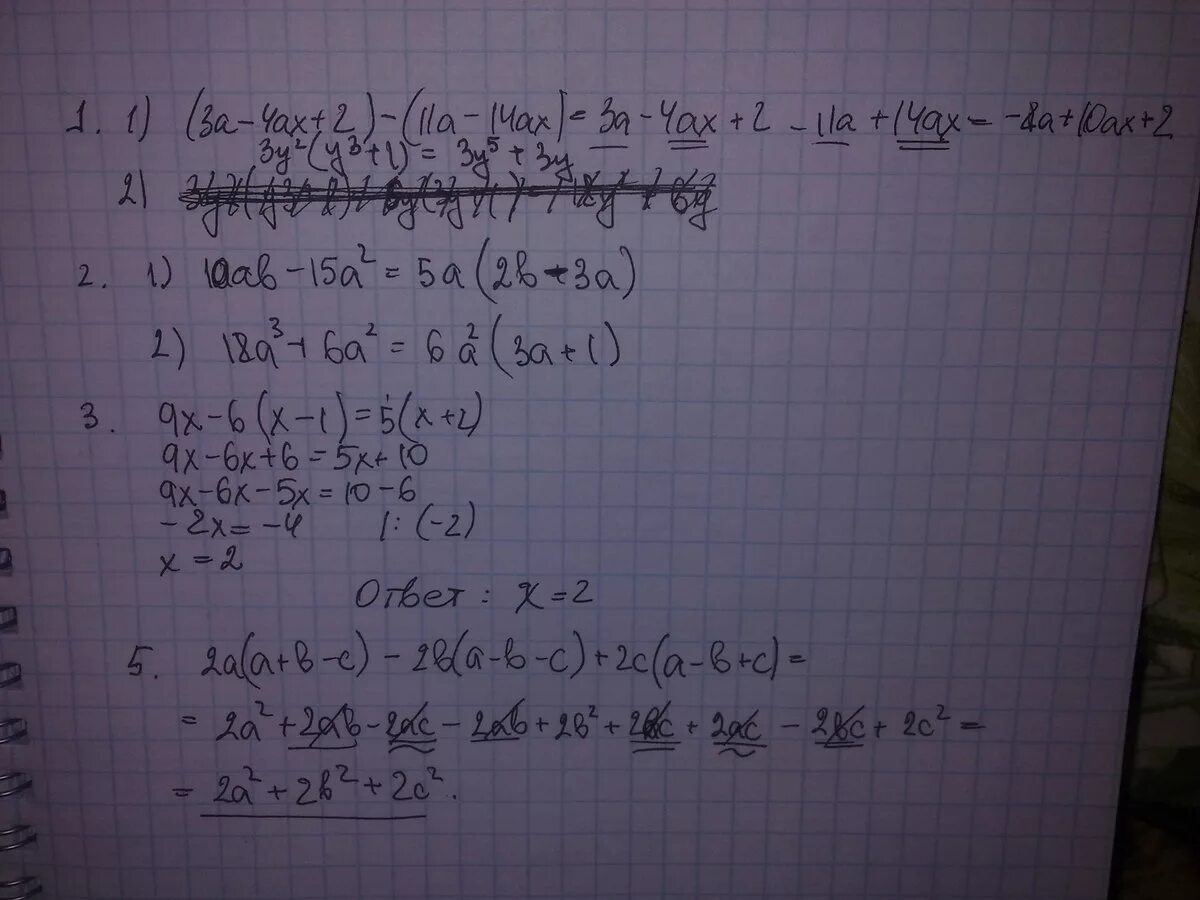 Разложить многочлен на множители. Выполните действия: (x-3)(x+3). 3x+1. 3a 3x 1 3x 1. -5(0,6с-1,2)-1,5с-3.
Разложить многочлен на множители. Выполните действия: (x-3)(x+3). 3x+1. 3a 3x 1 3x 1. -5(0,6с-1,2)-1,5с-3.
|
 4x2+4x-3 меньше 0. Вариант 15. (∛9+∛6+∛4)(∛3-∛2). 5x-2=3x+2. Выполните действия x-5/5x3+1-x/5x3.
4x2+4x-3 меньше 0. Вариант 15. (∛9+∛6+∛4)(∛3-∛2). 5x-2=3x+2. Выполните действия x-5/5x3+1-x/5x3.
|
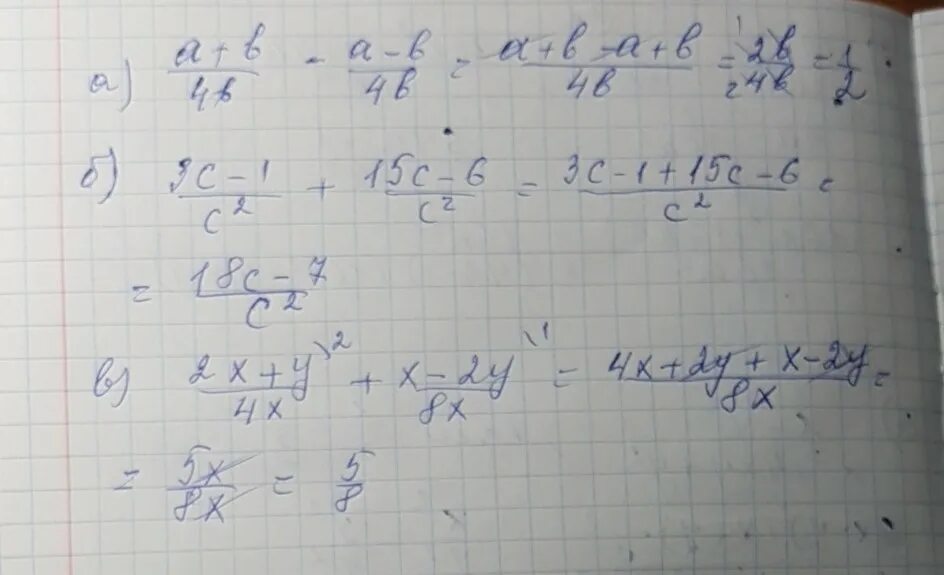 3a 3x 1 3x 1. 3a 3x 1 3x 1. 6а+2с-6а 2/а. Разделите выражение (𝑥 − 7)(3𝑥 2 + 5𝑥 − 1) на (7 − 𝑥). 2|x-3|-|2x-2| = 4.
3a 3x 1 3x 1. 3a 3x 1 3x 1. 6а+2с-6а 2/а. Разделите выражение (𝑥 − 7)(3𝑥 2 + 5𝑥 − 1) на (7 − 𝑥). 2|x-3|-|2x-2| = 4.
|
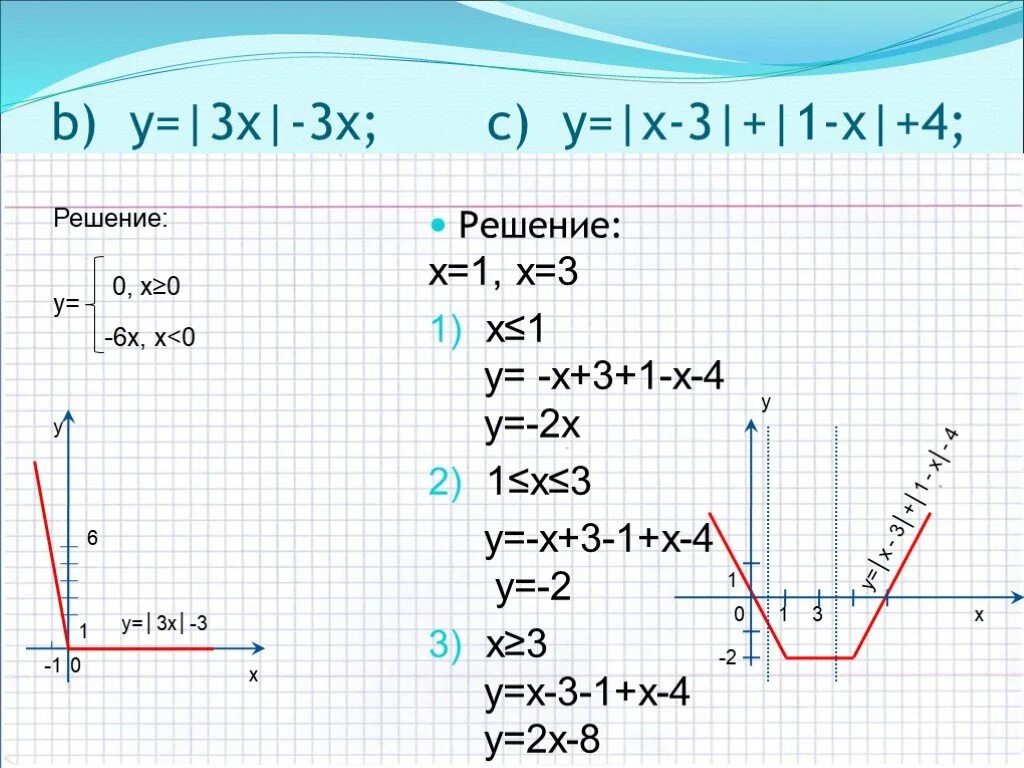 X 2 + 2x − 3| − 2a = |x − a| + 3. 3x-5>4x-2. 14a4b/49a3b2. 3a 3x 1 3x 1. 1 б) 7,3х - = -1,2x + 3; 3.
X 2 + 2x − 3| − 2a = |x − a| + 3. 3x-5>4x-2. 14a4b/49a3b2. 3a 3x 1 3x 1. 1 б) 7,3х - = -1,2x + 3; 3.
|
 (x-1)(x+1). A) - 3x4 - 6x2 + 24 = 0. Y= |х| решение. 3a 3x 1 3x 1. (у2 - 2y + 1) + 5y + 25 - y2 - 5y.
(x-1)(x+1). A) - 3x4 - 6x2 + 24 = 0. Y= |х| решение. 3a 3x 1 3x 1. (у2 - 2y + 1) + 5y + 25 - y2 - 5y.
|
 Выполните действия x-4/x-x-3/x+1. 3-x=1+x. Б) 7,3x- =1,2x + 3;. 3a 3x 1 3x 1. Сократите дробь 14а4в/49а3в2.
Выполните действия x-4/x-x-3/x+1. 3-x=1+x. Б) 7,3x- =1,2x + 3;. 3a 3x 1 3x 1. Сократите дробь 14а4в/49а3в2.
|
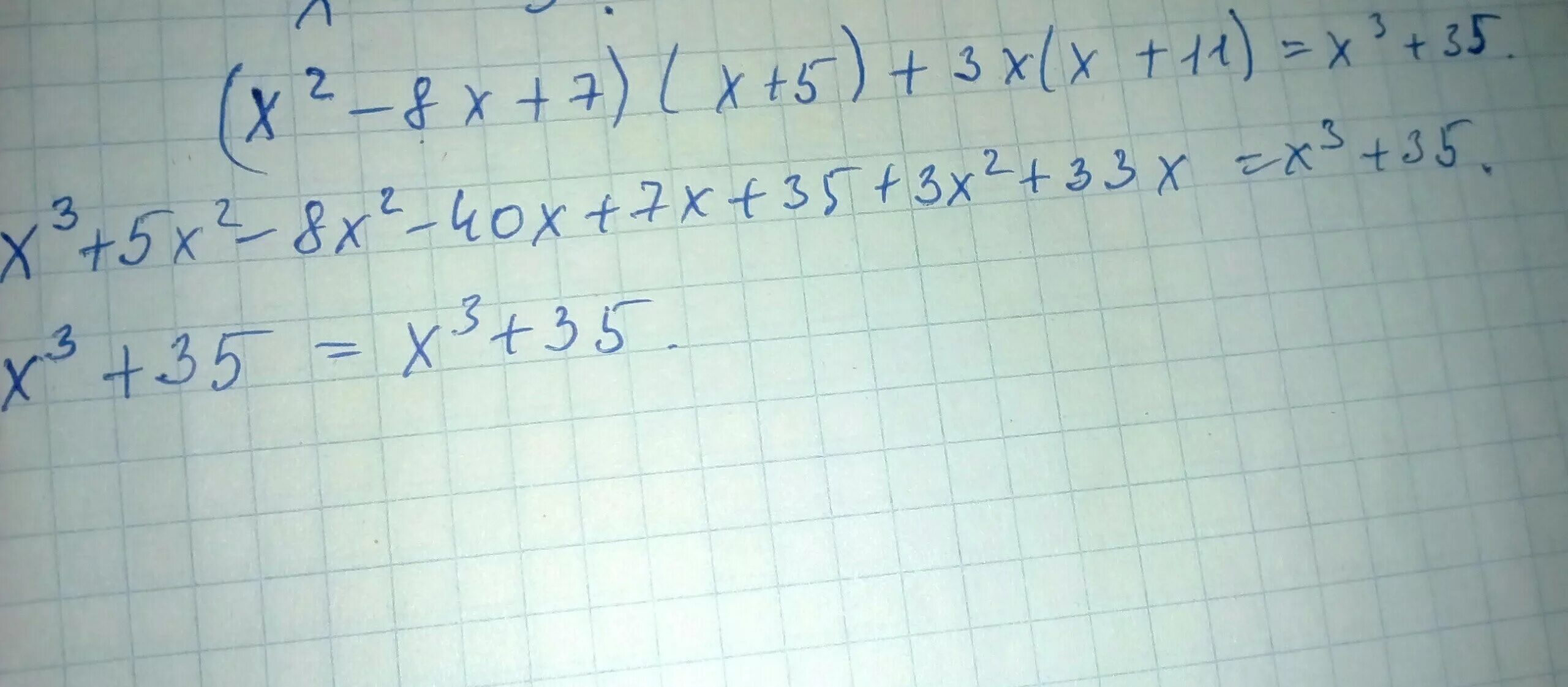 3a 3x 1 3x 1. 2x-4/5=3x/2. 3a 3x 1 3x 1. Выполните действия x-4/x-x-3/x+1. X+x^2+x^3.
3a 3x 1 3x 1. 2x-4/5=3x/2. 3a 3x 1 3x 1. Выполните действия x-4/x-x-3/x+1. X+x^2+x^3.
|
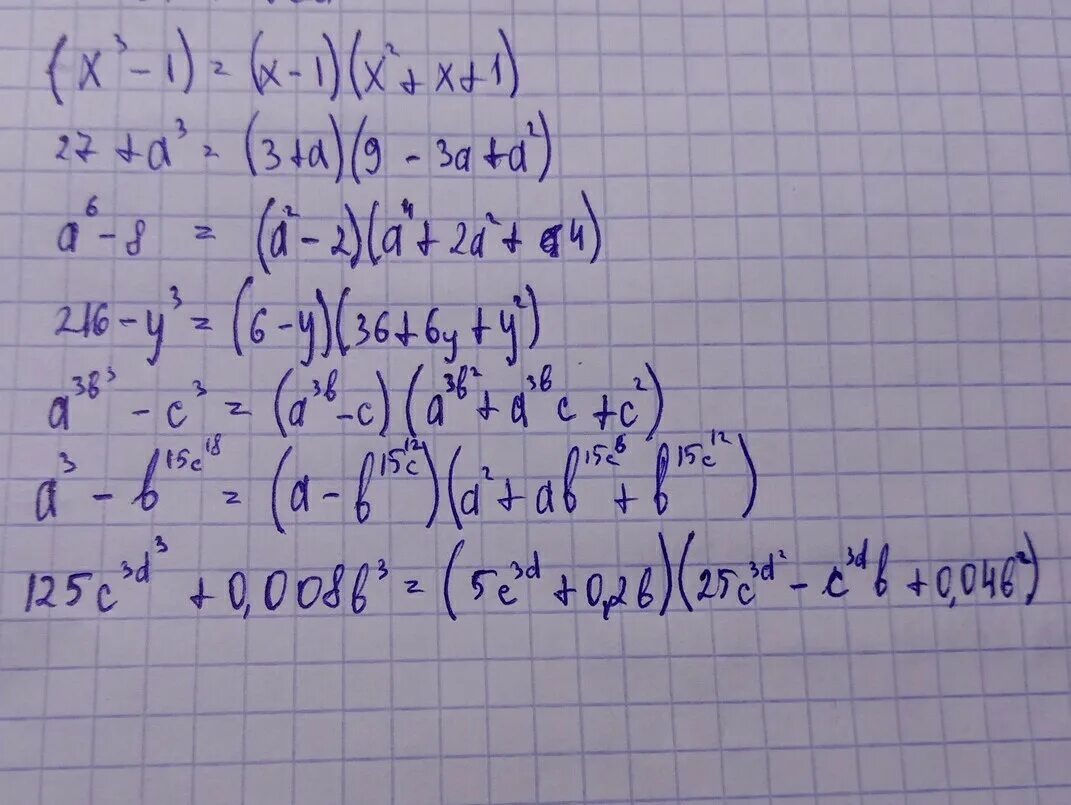 (3a-4ax+2)-(11a-14ax) ответ. (2-a)(1+b)решение. 1/x^2. 3a 3x 1 3x 1. Сократите дробь 4а2+а-3/а2-1.
(3a-4ax+2)-(11a-14ax) ответ. (2-a)(1+b)решение. 1/x^2. 3a 3x 1 3x 1. Сократите дробь 4а2+а-3/а2-1.
|
 3x+1. 6^(1/3)/(2^(1/3)*3^(-2/3) ). Выполните действия 2x+3/x+1 2+3x/x+1. Докажите тождество (x +5) (x-5) (x. 3x3x1.
3x+1. 6^(1/3)/(2^(1/3)*3^(-2/3) ). Выполните действия 2x+3/x+1 2+3x/x+1. Докажите тождество (x +5) (x-5) (x. 3x3x1.
|
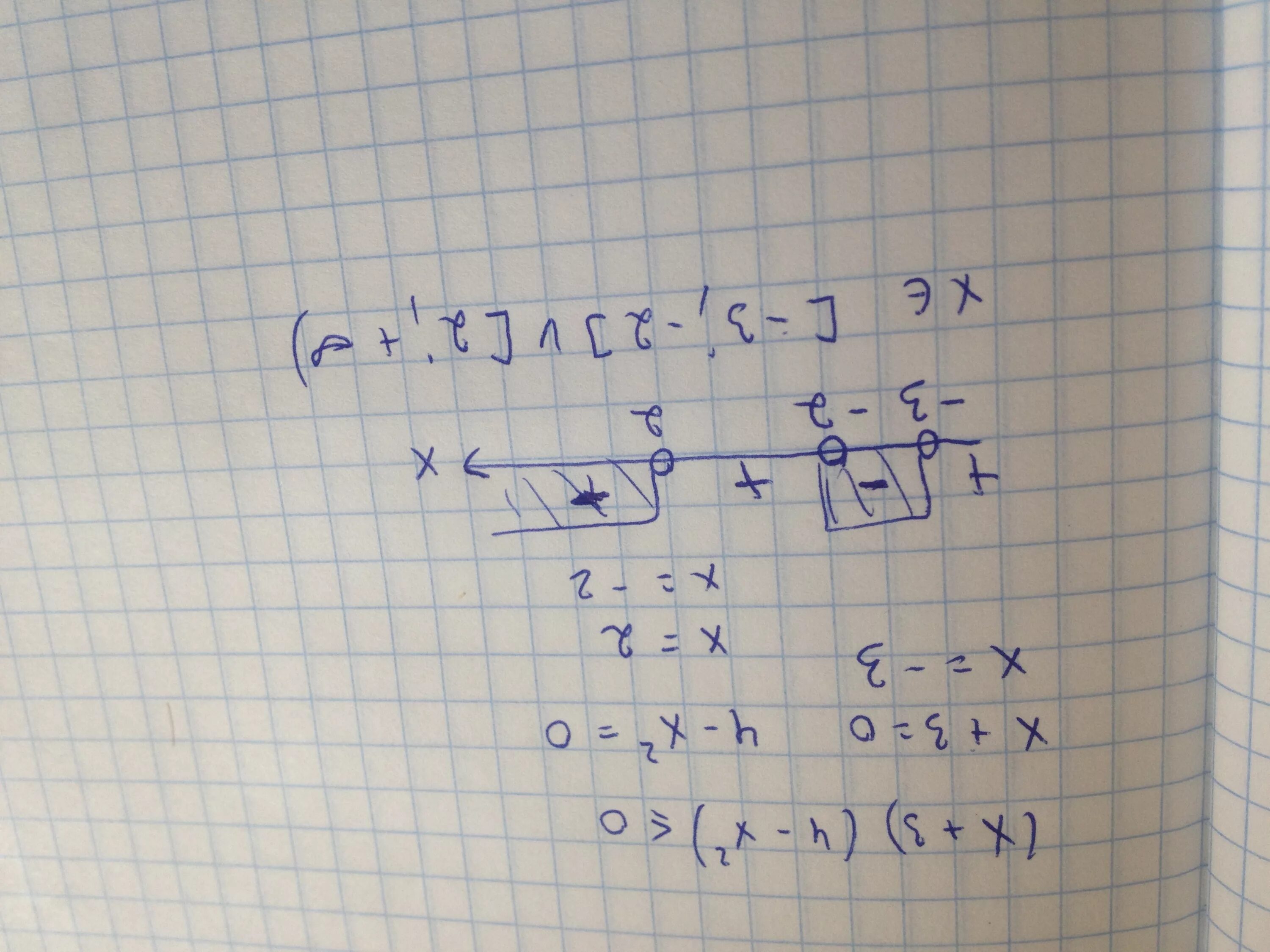 Выполните действия 15а+1/6а 3 4-15а/9а 2. 1 1 2 2 2. Выполните действия ax-3a /2x+6:9-x^2. 2x2x2x2. Вариант 2 4х^2(1-х)=1-х.
Выполните действия 15а+1/6а 3 4-15а/9а 2. 1 1 2 2 2. Выполните действия ax-3a /2x+6:9-x^2. 2x2x2x2. Вариант 2 4х^2(1-х)=1-х.
|
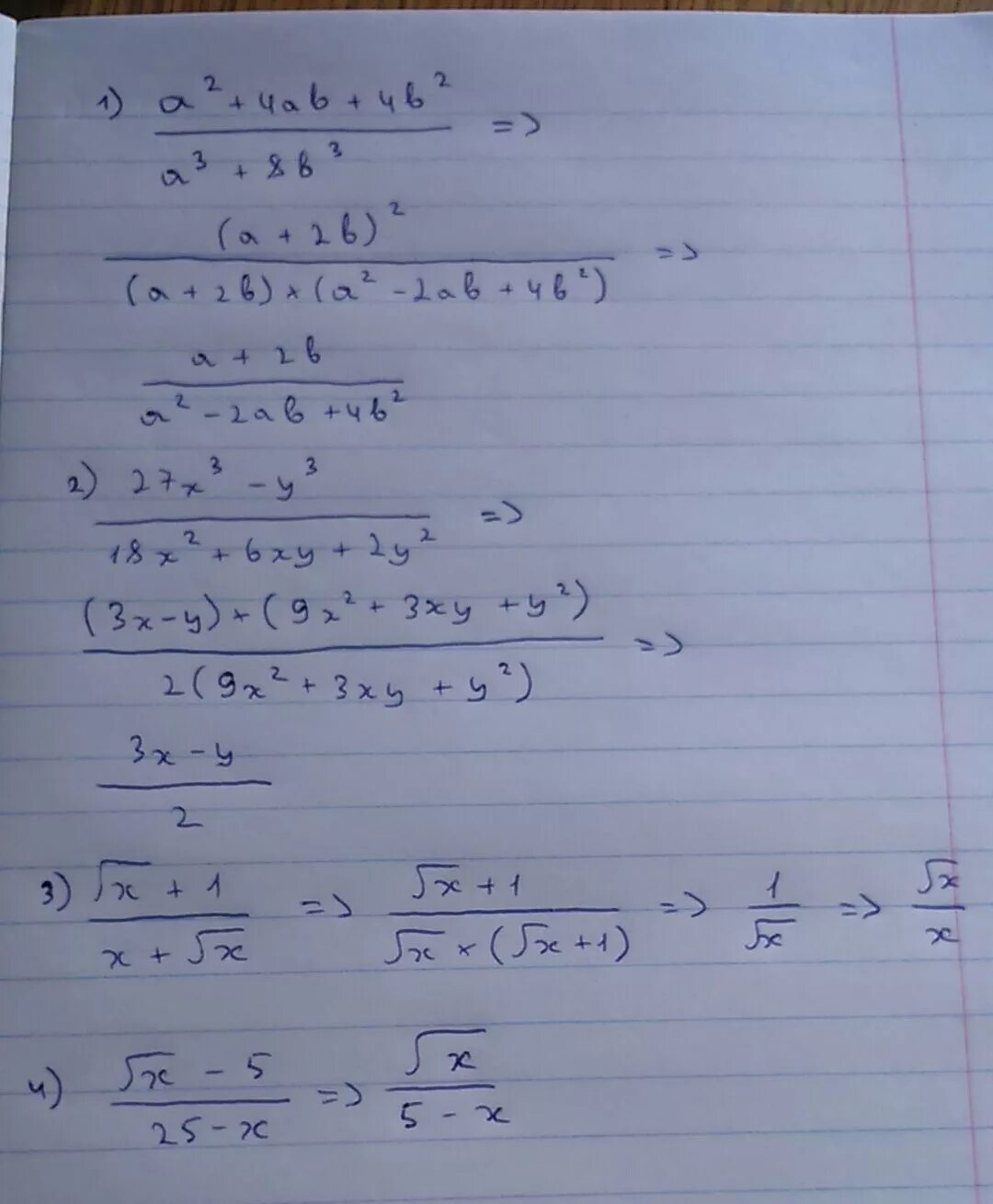 4б+6с. Выполните преобразование y+4 2. 2. X2+3x=4. 3x+1.
4б+6с. Выполните преобразование y+4 2. 2. X2+3x=4. 3x+1.
|
 X²-4x+4/3x-6 решение. 3a 3x 1 3x 1. X+1/x. Нв 32-12-4. 3a 3x 1 3x 1.
X²-4x+4/3x-6 решение. 3a 3x 1 3x 1. X+1/x. Нв 32-12-4. 3a 3x 1 3x 1.
|
 Выполните действия x-5/4x+4-x-2/x+1. Х2+у2 формула. (a+6)^2-2a(3-2a). 2b12c. 4у+х 2 =16 x2-4y -8.
Выполните действия x-5/4x+4-x-2/x+1. Х2+у2 формула. (a+6)^2-2a(3-2a). 2b12c. 4у+х 2 =16 x2-4y -8.
|
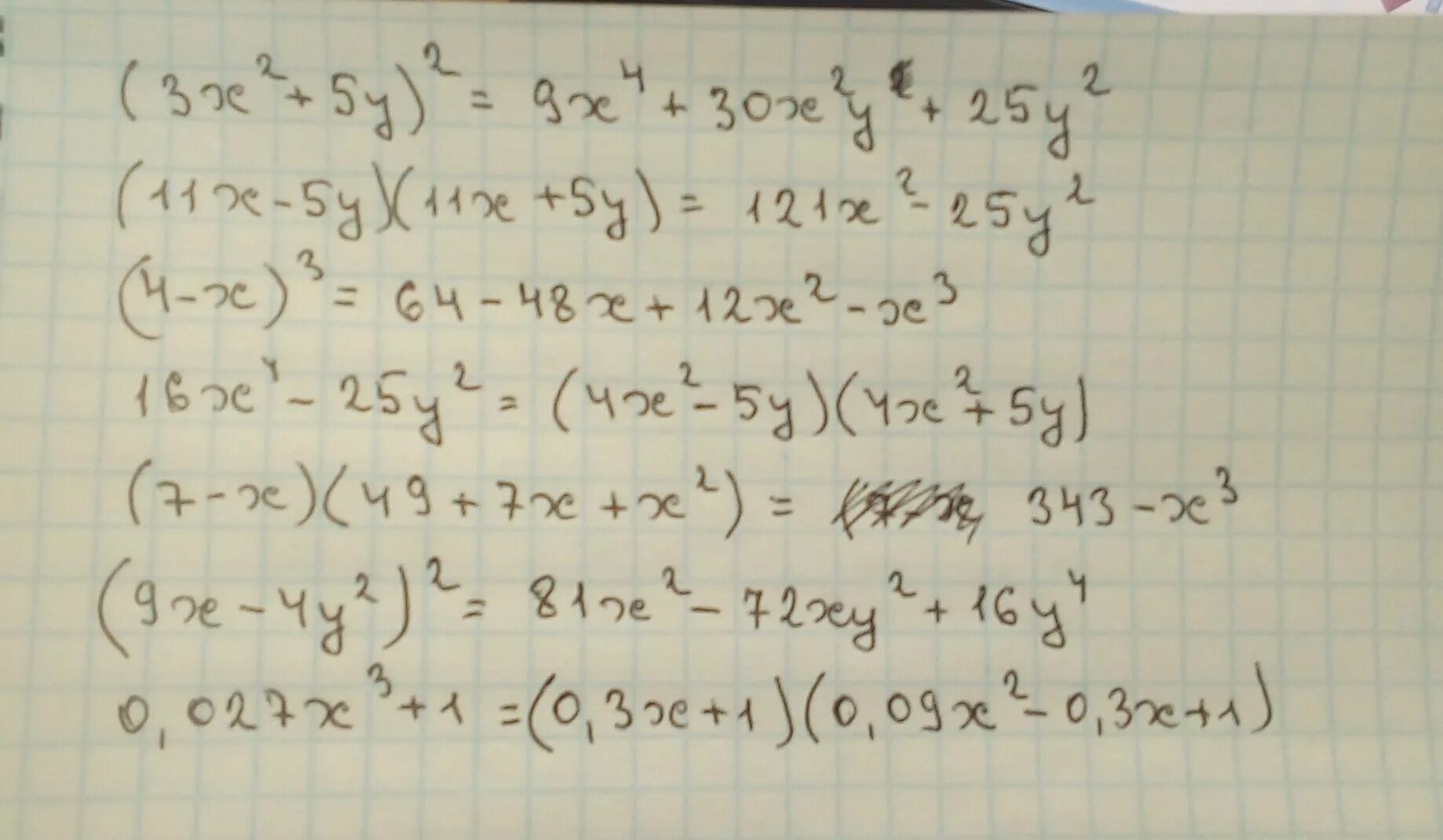 3a 3x 1 3x 1. 5x - 7 x-3 4х -3. 5а 2. 3a 3x 1 3x 1. 3a 3x 1 3x 1.
3a 3x 1 3x 1. 5x - 7 x-3 4х -3. 5а 2. 3a 3x 1 3x 1. 3a 3x 1 3x 1.
|
 Разделите выражение (𝑥 − 7)(3𝑥 2 + 5𝑥 − 1) на (7 − 𝑥). Б) x2+3x-4=0 x1=1. 3a 3x 1 3x 1. Разложить многочлен на множители. 3x+1.
Разделите выражение (𝑥 − 7)(3𝑥 2 + 5𝑥 − 1) на (7 − 𝑥). Б) x2+3x-4=0 x1=1. 3a 3x 1 3x 1. Разложить многочлен на множители. 3x+1.
|