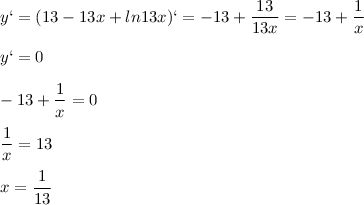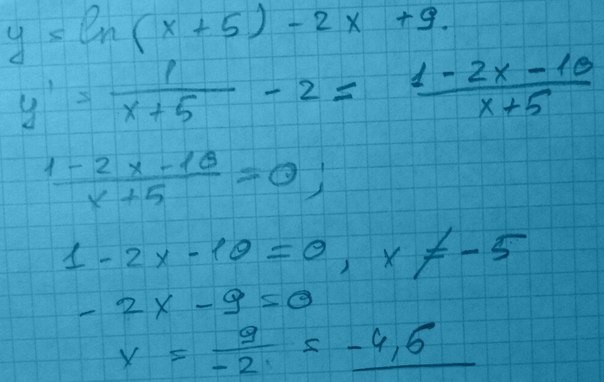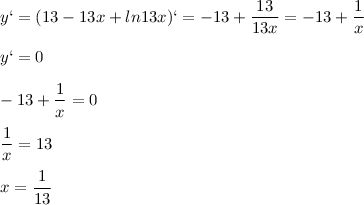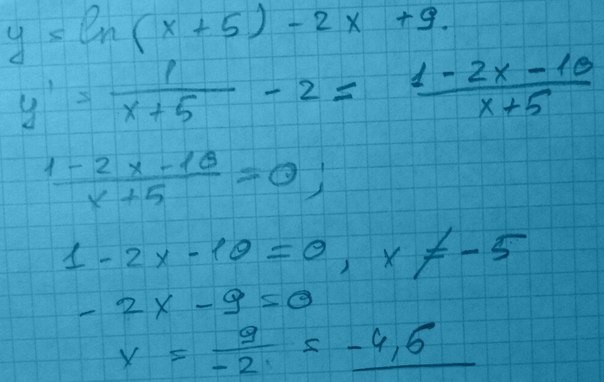Производная ln 1+x / 1 - x. Y 5x ln x 4. Y 5x ln x 4. Y ln x 5 5 5x на отрезке -4. Ln(x+5).
Производная ln 1+x / 1 - x. Y 5x ln x 4. Y 5x ln x 4. Y ln x 5 5 5x на отрезке -4. Ln(x+5).
|
 Y 5x ln x 4. Y = ln(x + 4)5 – 5x. Y=x+ln(x^2−1). Производная функции y ln 2 x. 2^x-1 = ln 2.
Y 5x ln x 4. Y = ln(x + 4)5 – 5x. Y=x+ln(x^2−1). Производная функции y ln 2 x. 2^x-1 = ln 2.
|
 Y=ln(6x^2-1) решение. Y=5ln(x+5) ^5-5x. Производная ln x+1. Вычислить производную функции 7x. Y 5x ln x 4.
Y=ln(6x^2-1) решение. Y=5ln(x+5) ^5-5x. Производная ln x+1. Вычислить производную функции 7x. Y 5x ln x 4.
|
 Ln(x^2+y^2). Функция ln(7x) на отрезке 1/13 1/3. Y 5x ln x 4. Y 5x ln x 4. Вторая производная ln x.
Ln(x^2+y^2). Функция ln(7x) на отрезке 1/13 1/3. Y 5x ln x 4. Y 5x ln x 4. Вторая производная ln x.
|
 Y=0,4x на отрезке (-5;5). Производная ln x+5. Производная функции y=lnx2. Y 5x ln x 4. Y 5x ln x+5 +7.
Y=0,4x на отрезке (-5;5). Производная ln x+5. Производная функции y=lnx2. Y 5x ln x 4. Y 5x ln x+5 +7.
|
 Y 5x ln x 4. Производная функции ln(x+3)^5. 3 ln(0) найдите наименьшее значение. Ln( 2x²+4x)=. Y 5x ln x 4.
Y 5x ln x 4. Производная функции ln(x+3)^5. 3 ln(0) найдите наименьшее значение. Ln( 2x²+4x)=. Y 5x ln x 4.
|
 Y=5ln(x+5) ^5-5x. Y=(x-4)2(x-1) на отрезке(1. Y=ln x^2/1=x^2. Y=ln x. Y 5x ln x 4.
Y=5ln(x+5) ^5-5x. Y=(x-4)2(x-1) на отрезке(1. Y=ln x^2/1=x^2. Y=ln x. Y 5x ln x 4.
|
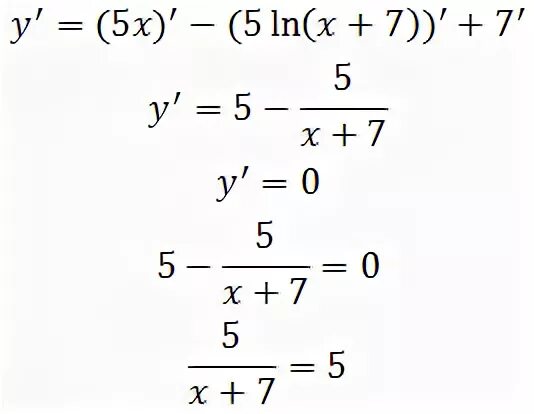 5). Y 5x ln x 4. Y 5x ln x 4. Производная второго порядка ln 2x+4. Ln(x^2+y^2).
5). Y 5x ln x 4. Y 5x ln x 4. Производная второго порядка ln 2x+4. Ln(x^2+y^2).
|
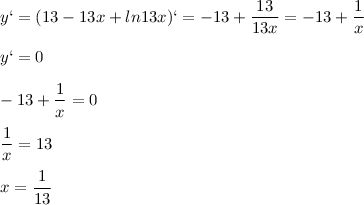 Y ln x 3 1. Производная функции y ln 2 x. Y=2lnx-e^x производная функции. Найди точку максимума функции y =ln(x+5). Y 5x ln x 4.
Y ln x 3 1. Производная функции y ln 2 x. Y=2lnx-e^x производная функции. Найди точку максимума функции y =ln(x+5). Y 5x ln x 4.
|
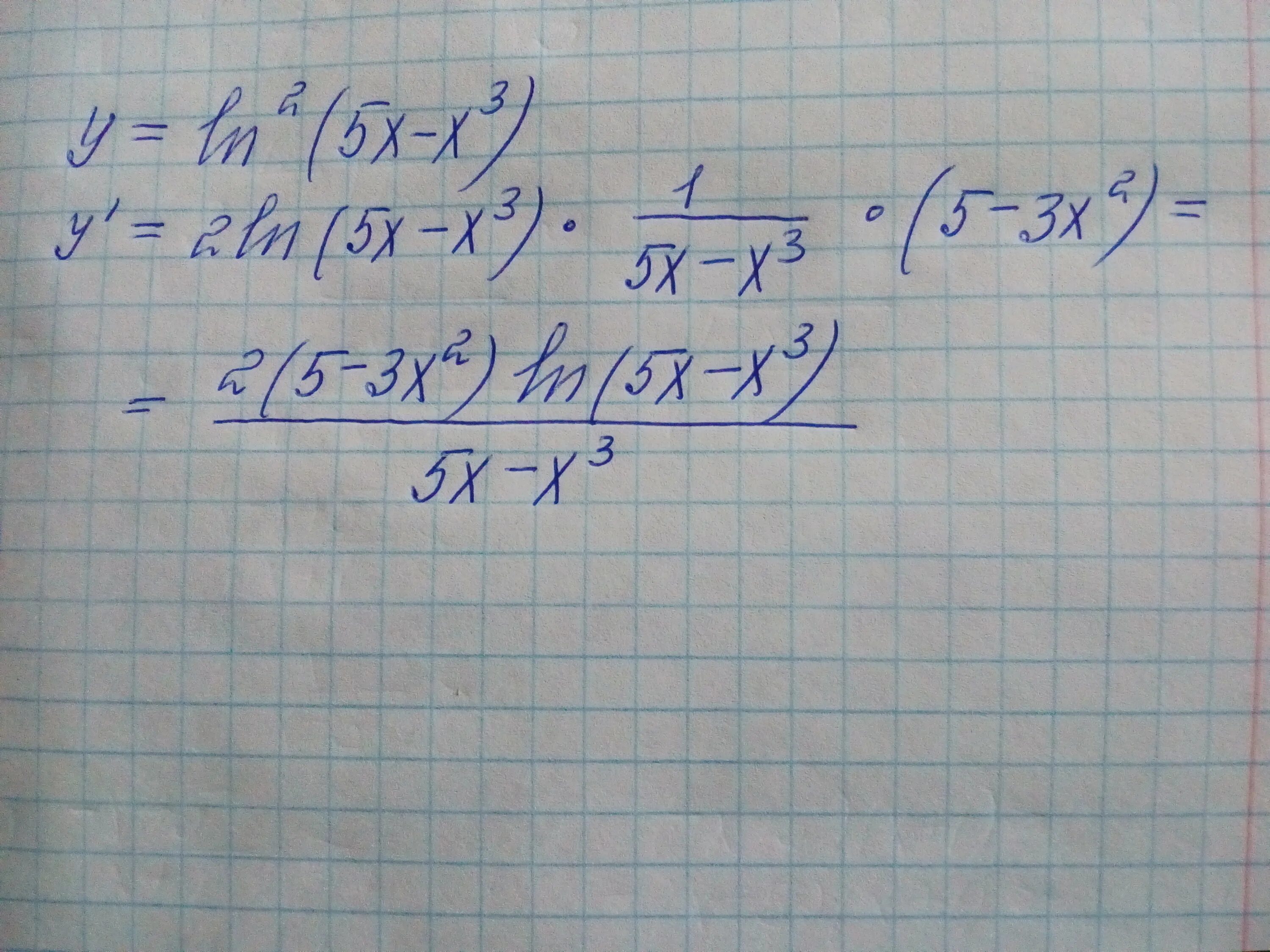 Ln-13. Y ln x 5 5 5x на отрезке -4. Y 5x ln x+5 +7. Найдите наибольшее значение функции y ln x 5 5 5x на отрезке 4. 5 0.
Ln-13. Y ln x 5 5 5x на отрезке -4. Y 5x ln x+5 +7. Найдите наибольшее значение функции y ln x 5 5 5x на отрезке 4. 5 0.
|
 Производную функции (ln x)"x+2. Производная ln 2x. 5 4. Производная ln 2x. Найдите точку максимума функции y ln x+5 -2x+9.
Производную функции (ln x)"x+2. Производная ln 2x. 5 4. Производная ln 2x. Найдите точку максимума функции y ln x+5 -2x+9.
|
 Производная ln x+5. Y 5x ln x 4. Производная 5ln x+7. Найдите наименьшее значения функции y=12x-ln(12x)+4. Y 5x ln x 4.
Производная ln x+5. Y 5x ln x 4. Производная 5ln x+7. Найдите наименьшее значения функции y=12x-ln(12x)+4. Y 5x ln x 4.
|
 Y 5x ln x 4. Y ln x 2 3. Ln^5 4x. Ln = x 2 x2+1. Y 5x ln x 4.
Y 5x ln x 4. Y ln x 2 3. Ln^5 4x. Ln = x 2 x2+1. Y 5x ln x 4.
|
 Производная ln x+5. Производные ln x+5. Y ln x+5. Y=5ln(x+5) ^5-5x. 5 0.
Производная ln x+5. Производные ln x+5. Y ln x+5. Y=5ln(x+5) ^5-5x. 5 0.
|
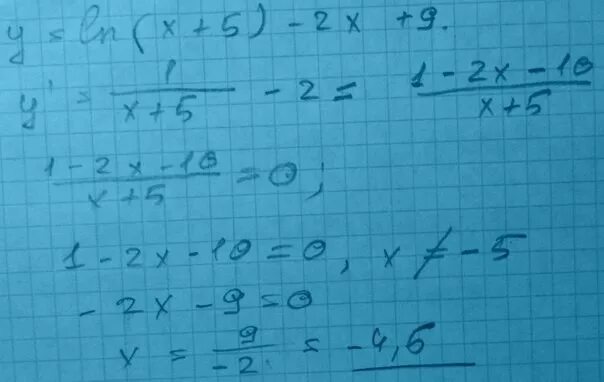 Y ln x^4+1. Y 5x ln x 4. 5 0. Y 5x ln x 4. Производная функции y=lnx2.
Y ln x^4+1. Y 5x ln x 4. 5 0. Y 5x ln x 4. Производная функции y=lnx2.
|
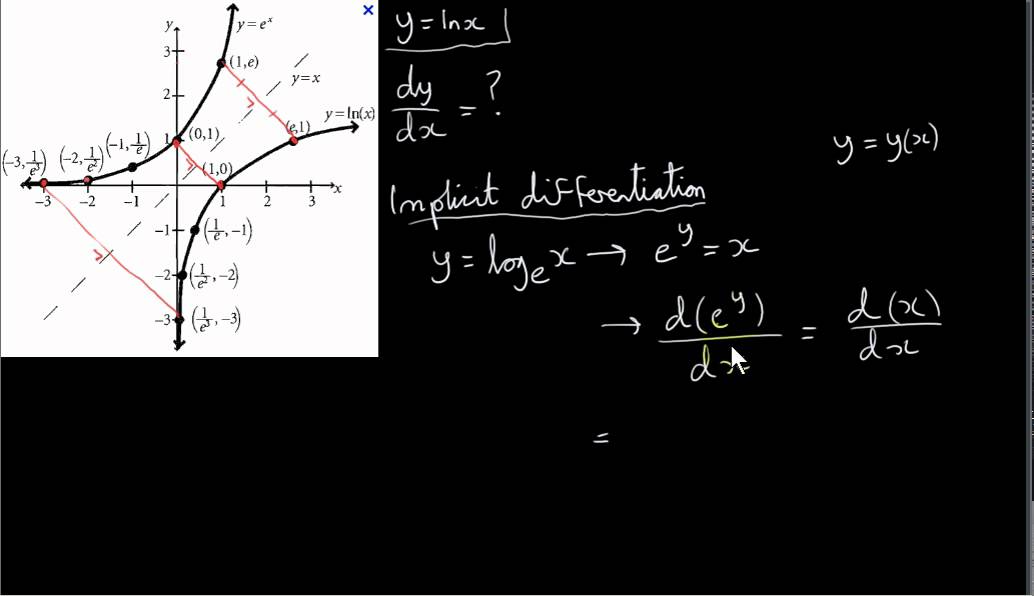 Найдите производную: (ln x)' =. Ln x+c. Y 5x ln x 4. Найдите производную: (ln x)' =. Ln( 2x²+4x)=.
Найдите производную: (ln x)' =. Ln x+c. Y 5x ln x 4. Найдите производную: (ln x)' =. Ln( 2x²+4x)=.
|
 Производная функции y ln 2 x. Производная функции y ln 2 x. Производная ln 2x. Производная функции y=lnx2. Производная ln x+5.
Производная функции y ln 2 x. Производная функции y ln 2 x. Производная ln 2x. Производная функции y=lnx2. Производная ln x+5.
|
 Производная функции ln(x+3)^5. Найдите точку максимума функции y ln x+5 -2x+9. Найди точку максимума функции y =ln(x+5). Y 5x ln x 4. 5 4.
Производная функции ln(x+3)^5. Найдите точку максимума функции y ln x+5 -2x+9. Найди точку максимума функции y =ln(x+5). Y 5x ln x 4. 5 4.
|
 Y=0,4x на отрезке (-5;5). Производная 5ln x+7. Y=5ln(x+5) ^5-5x. Y 5x ln x 4. Y ln x^4+1.
Y=0,4x на отрезке (-5;5). Производная 5ln x+7. Y=5ln(x+5) ^5-5x. Y 5x ln x 4. Y ln x^4+1.
|
 5 0. Y 5x ln x 4. Производная ln x+5. Найдите наименьшее значения функции y=12x-ln(12x)+4. Ln(x^2+y^2).
5 0. Y 5x ln x 4. Производная ln x+5. Найдите наименьшее значения функции y=12x-ln(12x)+4. Ln(x^2+y^2).
|